Zerosum Security
A history of public key cryptography
(under construction)
Zerosum Security
Early pioneers
Laying the foundations (1950s - 1960s)
Claude Shannon (Bell Labs, MIT) and Horst Feistel (MIT, IBM)


Martin Hellman
- Worked at IBM in 1968-1969 with Horst Feistel
- Professor at Stanford starting in 1971
- Thesis advisor of Whitfield Diffie and Ralph Merkle

Ralph Merkle
- Student at Berkeley in early seventies
- Ph.D. from Stanford, supervised by Martin Hellman
- First concrete ideas for PKC
- Besides PKC contributions, would have major influence in other cryptographic areas (inventing construction for hashing, Merkle trees, etc.)

Ralph Merkle
- Undergraduate taking CS244 Computer Security course at Berkeley
- Two project proposal by Merkle, first one contained idea of using puzzles, second one described vaguely the idea of trapdoor one-way functions. This proposal was rejected by lecturer (Lance Hoffman)

Merkle puzzles
- Secure communications over insecure channels
- Drafted in 1974, submitted in 1975, rejected several times, finally published in ACM in 1978
- Contained first asymmetric cryptosystem, based on symmetric crypto 'puzzles'

Merkle puzzles - an example
- Suppose Alice and Bob secretly want to establish a secret key over a public channel
- Alice generates \(m\) puzzles \(c_i\) by setting \[ c_i = E_{k_i}( r_i || s_i || 0_{2n})\] with \(E\) a strong symmetric encryption algorithm, \(k_i\) a random \(n\)-bit key, \(r_i\) a 128-bit identifier and \(s_i\) a 128-bit secret and \(0_{2n}\) are 2n zero bits, and sends them to Bob
- Alice keeps the pairs \(\{r_i,s_i\}\) stored
- Bob selects a random puzzle \(c_i\), tries all possible values for \(k_i\) until a plaintext is found with \(2n\) trailing zero bits
- Bob sends the recoverd identifier \(r_i\) to Alice, who looks up the corresponding value of \(s_i\), which is a secret they both know now
- On average, it will take Bob \(2^{n-1}\) trial decryption
- An eavesdropper doesn't know which puzzle Bob selected, so will have to try random puzzles
- This will take an eavesdropper on average roughly \(m/2 \cdot 2^{n}\) decryptions
- For example, when \(m \approx 2^n\), that is the square of the amount of work Bob had to do
Whitfield Diffie
- Student of Martin Hellman in early 70s
- Met Martin Hellman in summer of 1974
- Drafted in 1974, submitted in 1975, rejected several times, finally published in ACM in 1978
- Contained first asymmetric cryptosystem

Collaboration

New directions (1976)

Diffie-Hellman(-Merkle) key exchange
- Suppose Alice wants to agree on a shared secret over a public channel
- First Alice and Bob agree publicly on a group \(G\) and a generator \(g\)
- Alice generates a random number \(r_A\) and sends Bob \[ R_A = g^{r_A} \]
- Similarly, Bob generates a random number \(r_B\) and sends Alice \[ R_B = g^{r_B} \]
- Now, Alice and Bob can both compute \[s = g^{r_Ar_B} = R_A^{r_B} = R_B^{r_A}\]
- An eavesdropper sees only \(g_{r_A}\) and \(g_{r_B}\), best known method for an eavesdropper to construct \(s\) is to solve the discrete logarithm: recovering \(x\) from \(g^x\)
- In the original paper \(G = \mathbb{F}_p^*\) for a prime \(p\)
Meanwhile at MIT (1977)
Adi Shamir, Ron Rivest and Len Adleman

RSA (1977)

Vanilla RSA explained
- Suppose Alice wants to send a message \(m\) only Bob can read
- First Bob will generate two large primes \(p,q\) and computes the product \(N = pq\)
- Bob also generates a number \(e\) that has no divisors in common with both \(p-1\) and \(q-1\)
- Finally, Bob computes (via Chinese remainder theorem) \(d\) such that \[ ed = 1 \ ( \text{mod} \ (p-1)(q-1))\]
- Bob sends the pair \((N,e)\) to Alice and keeps \(d\) secret
- Alice sends Bob the ciphertext \(c\) with \[ c = m^e \ (\text{mod} \ N)\]
- Bob can recover \(m\) from \(c\) since basic number theory gives \[c^d = m^{ed} = m \ ( \text{mod} \ N)\]
- Best known method to recover \(m\) from just \(c\) is to first recover \(d \ \) by factoring \(N\).
RSA signatures
- Suppose Bob wants to sign a message \(m\) with his secret key \(d\) corresponding with his public key \((N,e)\)
- With a cryptographic hash function \(H\)), the message \(m\) is digested to \(h = H(m)\)
- Bob computes the signature \(s\) over \(m\) as \[ s = h^d \ (\text{mod} \ N)\]
- To verify the signature, anyone can recover \(h\) from \(s\) since \[s^e = h^{ed} = h \ ( \text{mod} \ N)\] and verify \(H(m) = h\)
- If the hash verifies, \(s\) can only have been constructed by Bob, since he is the only one knowing \(d\)
Taher Elgamal
- Student at Stanford of Martin Hellman in early 80s
- Basically made DH protocol non-interactive (1985)
- Elgamal encryption and digital signature scheme
- Digital signature scheme basis for (EC)DSA
- In the 90s, Elgamal (then at Netscape) was one of the drivers behind development of SSL

Elgamal hybrid encryption scheme
- Suppose Alice wants to send a message \(m\) only Bob can read
- First Alice and Bob will agree on group \(G\) with generator \(g\)
- Bob generates a secret key \(s_B\) and publishes the public key \(p_B = g^{s_B}\)
- Alice generates a random ephemeral key \(r_A\) and computes the message key \[k = p_B^{r_A} = g^{s_Br_A}\]
- Finally, Alice sends Bob the pair \((g^{r_A}, E_k(m))\) with \(E\) a symmetric encryption algorithm
- Bob can recompute \(k\) as \[ (g_{r_A})^{s_B} = g^{r_As_B} = k\] and decrypt \(E_k(m)\) to recover \(m\)
- In the original paper \(G = \mathbb{F}_p^*\) for a prime \(p\) and \(E: (k,m) \to k \cdot m \in G\)
Elgamal signature scheme
- Let \(H\) be a cryptographic hash function, \(p\) a large prime and a \(g\) generator of \(\mathbb{F}_p^*\)
- Suppose Bob wants to sign a message \(m\) with his secret key \(s_B\), with \(p_B = g^{s_B}\) his public key
- First, the message \(m\) is digested to \(h = H(m)\)
- Bob generates a random number \(k\) and computes \(r = g^k\)
- The signature then consists of the pair \((r,s)\) with \[s = \frac{h - r \cdot s_B}{k} \ \ \text{mod} \ (p-1)\]
- To verify the signature \((r,s)\) on \(m\) one computes \(h = H(m)\) and verfies that \[ g^h = p_B^r \cdot r^s \]
- This works since \[ p_B^r \cdot r^s = g^{rs_B} \cdot g^{ks} = g^{rs_B} \cdot g^{h - r \cdot s_B} = g^h \]
Other constructions
- Based on coding theory
- Based on knapsack problems
- Based on problems on lattices
- Bob generates a random number \(k\) and computes \(r = g^k\)
- The signature then consists of the pair \((r,s)\) with \[s = \frac{h - r \cdot s_B}{k} \ \ \text{mod} \ (p-1)\]
- To verify the signature \((r,s)\) on \(m\) one computes \(h = H(m)\) and verfies that \[ g^h = p_B^r \cdot r^s \]
- This works since \[ p_B^r \cdot r^s = g^{rs_B} \cdot g^{ks} = g^{rs_B} \cdot g^{h - r \cdot s_B} = g^h \]
Finding better DL groups
- Original DH was defined in the group \(\mathbb{F}_p^*\)
- DH construction works in \(\it{any}\) group in which discrete logarithms are hard
- Maybe there are group in which discrete logarihms are even harder
- The group \(\mathbb{F}_p^*\) can be trivially mapped to \(\mathbb{Z}\)
- Most efficient attacks on DL in \(\mathbb{F}_p^*\) - index calculus based algorithms - use this mapping
Maybe there are groups in which
- Normal computations are efficient - Discrete logarihms are hard - No easy constructable factor base to use in index calculus
Hendrik Lenstra (1985)
- Developed elliptic curve factorization method (ECM)
- Generalizes know weak case when either \(q\pm1\) or \(p\pm1\) is smooth to factor \(N = pq\)
- Generate random elliptic curve, if group order modulo either \(p\) or \(q\) is smooth, can factor \(N\)
- Big benefit: can try many curves

Elliptic curves (1985)
Victor Miller (IBM) and Neal Koblitz (University Washington), inspired by Lenstra's ECM, independently propose using these groups defined by elliptic curves for a DL setting.


Elliptic curves (1985)
Big driver: no obvious factor base in these groups to base an index calculus attack method on.
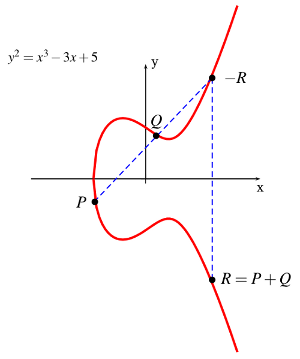
Elliptic curves (1985)
- When avoiding weak cases, there is no better algorithm known to attack the DL in elliptic curve groups than generic algorithm.

A not-so-secret-anymore secret history
Earlier at GCHQ

James Ellis conceived the concept of Non-Secret Encryption (NSE) in 1969, inspired by research from Bell labs.
Clifford Cocks (1973)


Clifford Cocks (1973)
- Only few months at GCHQ, heard of Ellis' idea
- Written down in half an hour
- Special case of RSA in which \(e=N\)

Malcolm Williamson
- Colleague, old friend and flatmate of Clifford Cocks
- Math Olympiad '68
- Tried to dispute Cocks' scheme
- Came up with what would become known as Diffie-Hellman key-exchange instead

Further reading
A new era
Mission accomplished?

Enter quantum algorithms
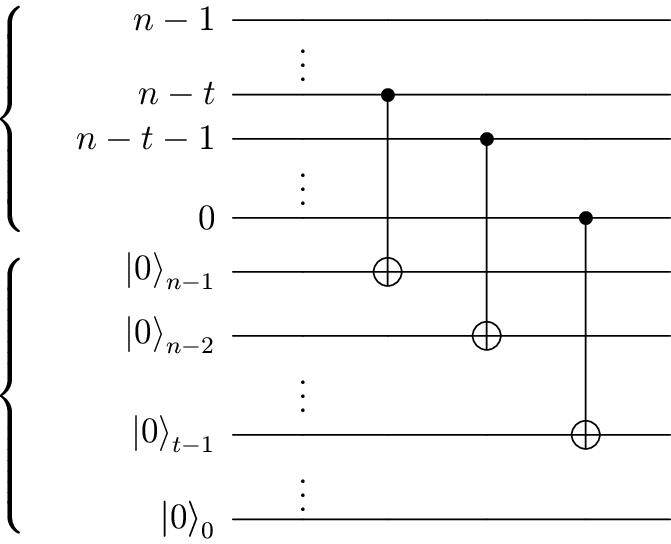
..and enter Peter Shor (1994)

Lattice based crypto
VMiklox Atjai (IBM) introduced lattice based cryptography, quickly joined by Cynthia Dwork. In 1997 they introduced the first lattice based cryptosystem.

